Prompt

fast fourier transformation (FFT)에 대해 이해하고 싶습니다. 진폭과 주파수가 다른 sine과 cosine 웨이브들을 각각 5개씩 더한 입력 데이터를 만들고, 이 데이터를 FFT하여 결과에서 입력한 진폭과 주파수를 확인하는 파이썬 예제를 부탁합니다. 그래프는 plotly로 그려주세요.

Response

FFT를 사용하여 신호를 분석하는 예제를 만들어보겠습니다.

import numpy as np
import plotly.graph_objects as go
from plotly.subplots import make_subplots

# 시간 도메인 설정
t = np.linspace(0, 1, 1000)

# 입력 신호 생성 (5개의 sine과 5개의 cosine 파형)
amplitudes_sin = [1.0, 0.8, 0.6, 0.4, 0.2]
frequencies_sin = [5, 10, 15, 20, 25]
amplitudes_cos = [0.9, 0.7, 0.5, 0.3, 0.1]
frequencies_cos = [7, 12, 17, 22, 27]

signal = np.zeros_like(t)
for amp, freq in zip(amplitudes_sin, frequencies_sin):
    signal += amp * np.sin(2 * np.pi * freq * t)
for amp, freq in zip(amplitudes_cos, frequencies_cos):
    signal += amp * np.cos(2 * np.pi * freq * t)

# FFT 수행
n = len(t)
fft_result = np.fft.fft(signal)
frequencies = np.fft.fftfreq(n, t[1] - t[0])
magnitudes = np.abs(fft_result) / n * 2

# 플롯 생성
fig = make_subplots(rows=2, cols=1, subplot_titles=('Time Domain Signal', 'Frequency Domain (FFT)'))

# 시간 도메인 신호 플롯
fig.add_trace(
    go.Scatter(x=t, y=signal, name='Signal'),
    row=1, col=1
)

# 주파수 도메인 플롯 (양의 주파수만)
positive_freq_mask = frequencies >= 0
fig.add_trace(
    go.Scatter(
        x=frequencies[positive_freq_mask],
        y=magnitudes[positive_freq_mask],
        name='FFT Magnitude'
    ),
    row=2, col=1
)

# 레이아웃 설정
fig.update_layout(
    height=800,
    showlegend=True,
    title_text="Signal Analysis with FFT"
)
fig.update_xaxes(title_text="Time (s)", row=1, col=1)
fig.update_xaxes(title_text="Frequency (Hz)", row=2, col=1)
fig.update_yaxes(title_text="Amplitude", row=1, col=1)
fig.update_yaxes(title_text="Magnitude", row=2, col=1)

fig.show()

이 코드는:

주어진 진폭과 주파수로 신호를 생성
FFT를 수행하여 주파수 성분 분석
시간 도메인과 주파수 도메인 그래프를 생성

주파수 도메인 그래프에서 입력한 주파수(5, 7, 10, 12, 15, 17, 20, 22, 25, 27 Hz)에서 피크가 나타나며, 피크의 높이는 입력한 진폭과 일치합니다.

실행 결과

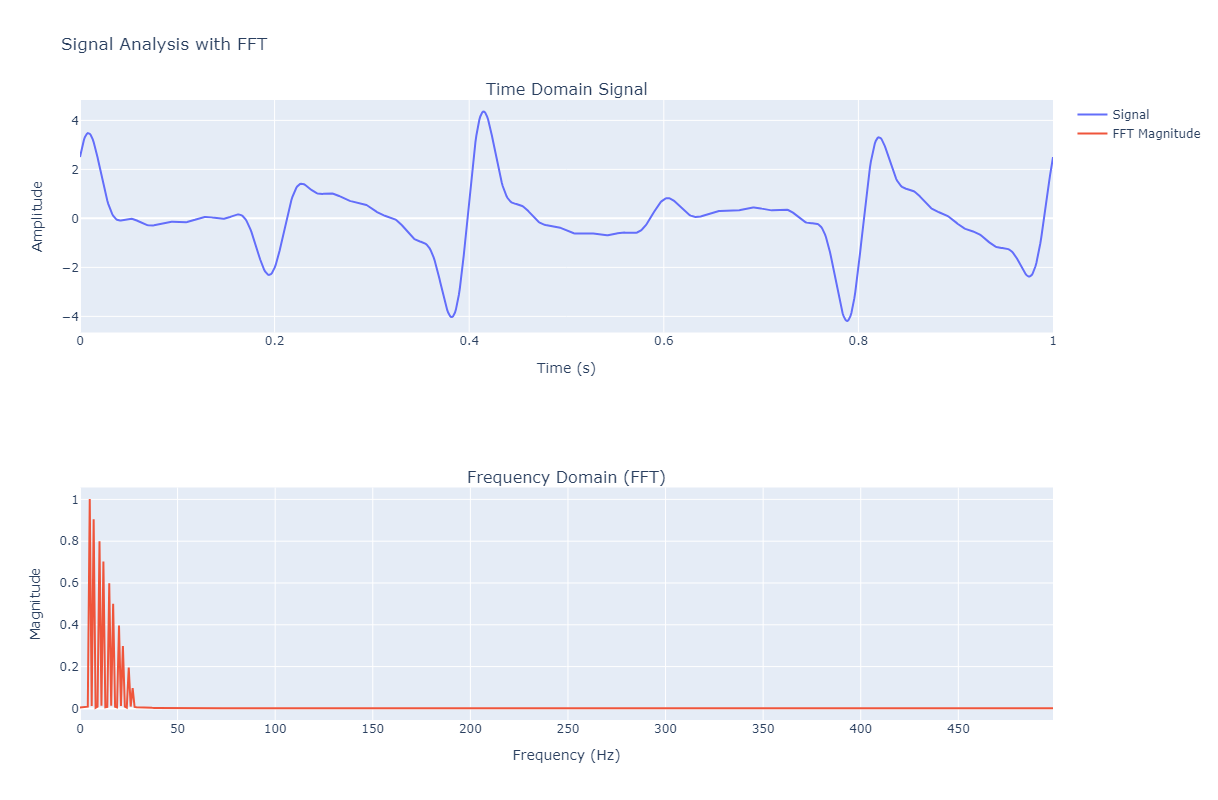
주파수를 잘 보기 위해 주파수 도메일 그래프를 확대
주파수와 진폭 결과를 별도로 출력하지 않았다.